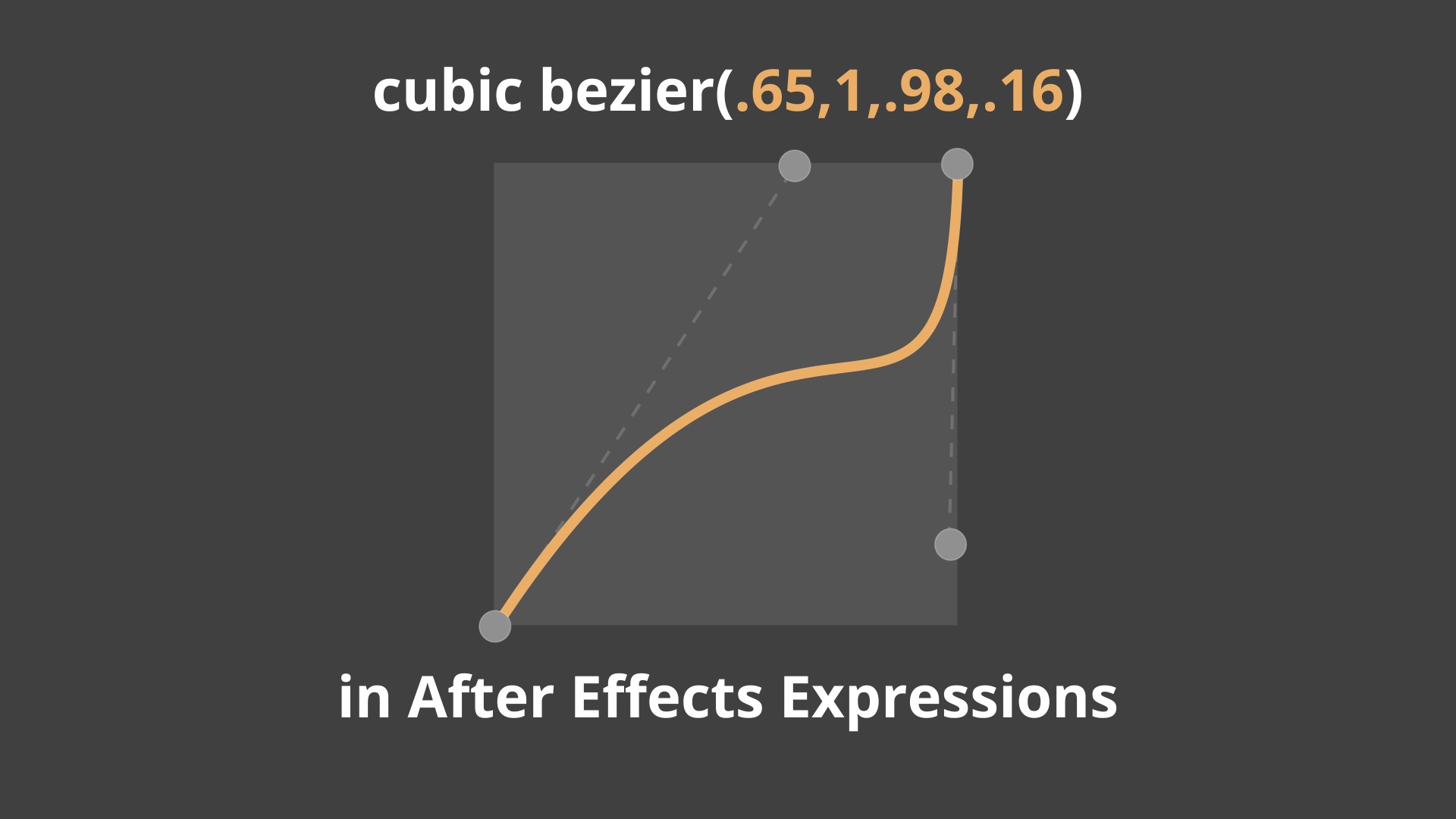
cubicEase. A new ease function inside expressions.

On 11-17-2020 I published an approach to use cubic-bezier curves inside After Effects expressions.
Now wrapped everything around a new function which can be used as an alternative to the regular ease-function.
It just comes with a new parameter, the cubic bezier values:

cubicEase(time, startTime , endTime, valueMin, valueMax, [cubic-bezier-values]);

An example on a path trim:

cubicEase(time, 0 , 2, 0, 100, [1, 0, 0.9, 0]);

And here is the minified function to use in an expression.

function cubicEase(IN,start,end,newStart,newEnd,bezier){var NEWTON_ITERATIONS=4;var NEWTON_MIN_SLOPE=0.001;var SUBDIVISION_PRECISION=0.0000001;var SUBDIVISION_MAX_ITERATIONS=10;var kSplineTableSize=11;var kSampleStepSize=1.0/(kSplineTableSize-1.0);var float32ArraySupported=false;function A(aA1,aA2){return 1.0-3.0*aA2+3.0*aA1}function B(aA1,aA2){return 3.0*aA2-6.0*aA1}function C(aA1){return 3.0*aA1}function calcBezier(aT,aA1,aA2){return((A(aA1,aA2)*aT+B(aA1,aA2))*aT+C(aA1))*aT}function getSlope(aT,aA1,aA2){return 3.0*A(aA1,aA2)*aT*aT+2.0*B(aA1,aA2)*aT+C(aA1)}function binarySubdivide(aX,aA,aB){var currentX,currentT,i=0;do{currentT=aA+(aB-aA)/2.0;currentX=calcBezier(currentT,mX1,mX2)-aX;if(currentX>0.0){aB=currentT}else{aA=currentT}}while(Math.abs(currentX)>SUBDIVISION_PRECISION&& ++i<SUBDIVISION_MAX_ITERATIONS);return currentT}function BezierEasing(mX1,mY1,mX2,mY2){if(arguments.length!==4){throw new Error("BezierEasing requires 4 arguments.")}for(var i=0;i<4;i+=1){if(typeof arguments[i]!=="number"||isNaN(arguments[i])||!isFinite(arguments[i])){throw new Error("BezierEasing arguments should be integers.")}}if(mX1<0||mX1>1||mX2<0||mX2>1){throw new Error("BezierEasing x values must be in [0, 1] range.")}var mSampleValues=float32ArraySupported?new Float32Array(kSplineTableSize):[kSplineTableSize];function newtonRaphsonIterate(aX,aGuessT){for(var i=0;i<NEWTON_ITERATIONS;i+=1){var currentSlope=getSlope(aGuessT,mX1,mX2);if(currentSlope===0.0){return aGuessT}var currentX=calcBezier(aGuessT,mX1,mX2)-aX;aGuessT-=currentX/currentSlope}return aGuessT}function calcSampleValues(){for(var i=0;i<kSplineTableSize;i+=1){mSampleValues[i]=calcBezier(i*kSampleStepSize,mX1,mX2)}}function getTForX(aX){var intervalStart=0.0;var currentSample=1;var lastSample=kSplineTableSize-1;for(;currentSample!=lastSample&&mSampleValues[currentSample]<=aX;currentSample+=1){intervalStart+=kSampleStepSize}currentSample-=1;var dist=(aX-mSampleValues[currentSample])/(mSampleValues[currentSample+1]-mSampleValues[currentSample]);var guessForT=intervalStart+dist*kSampleStepSize;var initialSlope=getSlope(guessForT,mX1,mX2);if(initialSlope>=NEWTON_MIN_SLOPE){return newtonRaphsonIterate(aX,guessForT)}else if(initialSlope===0.0){return guessForT}else{return binarySubdivide(aX,intervalStart,intervalStart+kSampleStepSize)}}var _precomputed=false;function precompute(){_precomputed=true;if(mX1!=mY1||mX2!=mY2){calcSampleValues()}}var f=function(aX){if(!_precomputed){precompute()}if(mX1===mY1&&mX2===mY2){return aX;}if(aX===0){return 0}if(aX===1){return 1}return calcBezier(getTForX(aX),mY1,mY2)};f.getControlPoints=function(){return[{x:mX1,y:mY1},{x:mX2,y:mY2}]};var args=[mX1,mY1,mX2,mY2];var str="BezierEasing("+args.join()+")";f.toString=function(){return str};var css="cubic-bezier("+args.join()+")";f.toCSS=function(){return css};f.toString=function(){return args};return f}var newValues=BezierEasing(bezier[0],bezier[1],bezier[2],bezier[3]);var AniTimerange=linear(IN,start,end,0,1);return linear(newValues(AniTimerange),0,1,newStart,newEnd)}

If you want to have a look into the code, visit my reposit on Github: cubicEase-for-After-Effects