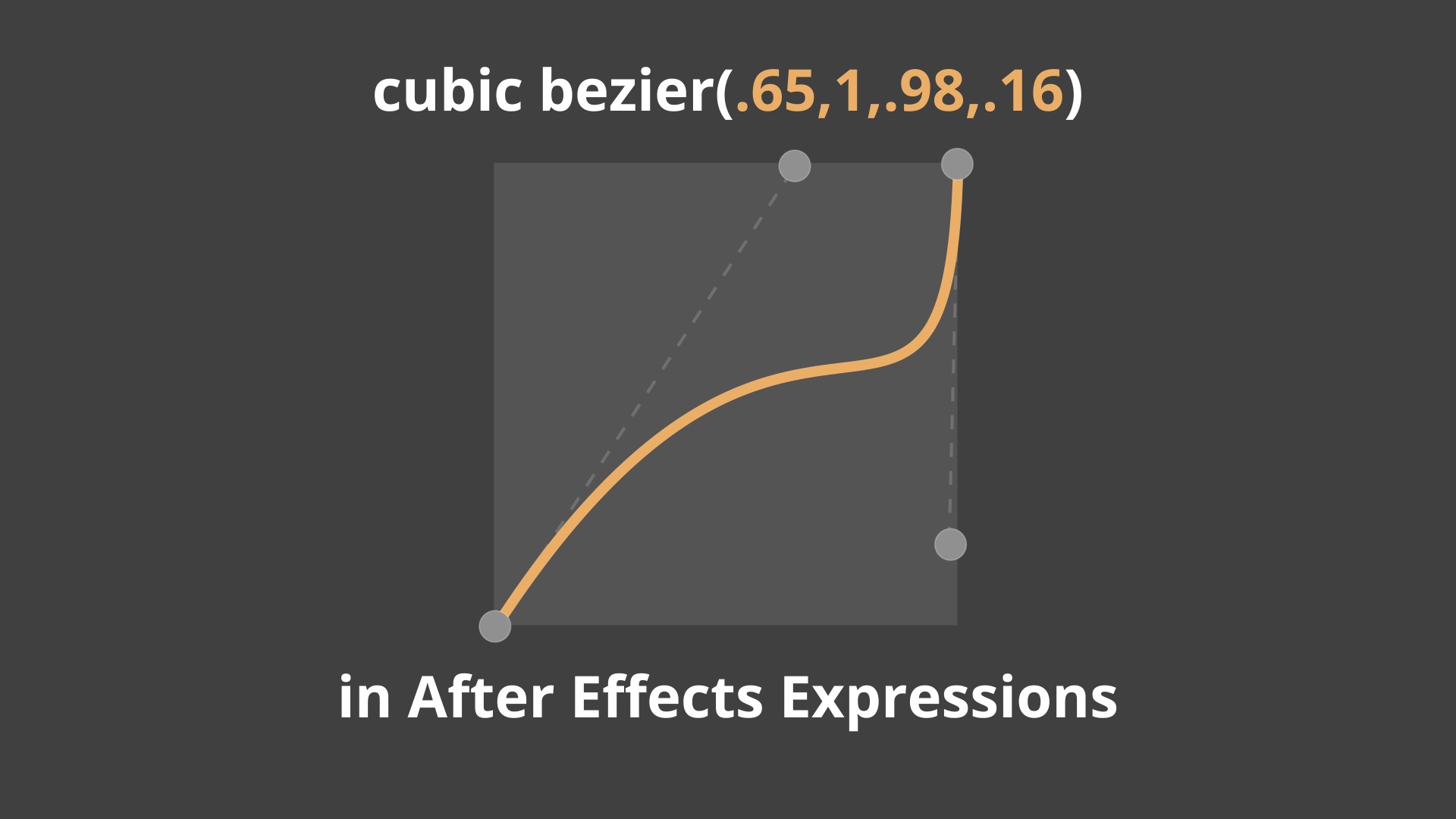
cubicEase. Eine neue ease-Funktion für Expressions.

Am 17.11.2020 habe ich eine Methode vorgestellt, wie man Cubic Bezier Werte in After Effects expressions verwenden kann.
Jetzt habe ich alles in eine eigene Funktion gepackt, welche der ease-Funktion gleich kommt.
Hinzugekommen ist ein neuer Parameter für die Cubic Bezier-Werte:

cubicEase(time, startTime , endTime, valueMin, valueMax, [cubic-bezier-values]);

Ein Beispiel auf einem Trim-Pfad:

cubicEase(time, 0 , 2, 0, 100, [1, 0, 0.9, 0]);

Angehängt eine minified Version der Funktion zur Verwendung innerhalb einer Expression.

function cubicEase(IN,start,end,newStart,newEnd,bezier){var NEWTON_ITERATIONS=4;var NEWTON_MIN_SLOPE=0.001;var SUBDIVISION_PRECISION=0.0000001;var SUBDIVISION_MAX_ITERATIONS=10;var kSplineTableSize=11;var kSampleStepSize=1.0/(kSplineTableSize-1.0);var float32ArraySupported=false;function A(aA1,aA2){return 1.0-3.0*aA2+3.0*aA1}function B(aA1,aA2){return 3.0*aA2-6.0*aA1}function C(aA1){return 3.0*aA1}function calcBezier(aT,aA1,aA2){return((A(aA1,aA2)*aT+B(aA1,aA2))*aT+C(aA1))*aT}function getSlope(aT,aA1,aA2){return 3.0*A(aA1,aA2)*aT*aT+2.0*B(aA1,aA2)*aT+C(aA1)}function binarySubdivide(aX,aA,aB){var currentX,currentT,i=0;do{currentT=aA+(aB-aA)/2.0;currentX=calcBezier(currentT,mX1,mX2)-aX;if(currentX>0.0){aB=currentT}else{aA=currentT}}while(Math.abs(currentX)>SUBDIVISION_PRECISION&& ++i<SUBDIVISION_MAX_ITERATIONS);return currentT}function BezierEasing(mX1,mY1,mX2,mY2){if(arguments.length!==4){throw new Error("BezierEasing requires 4 arguments.")}for(var i=0;i<4;i+=1){if(typeof arguments[i]!=="number"||isNaN(arguments[i])||!isFinite(arguments[i])){throw new Error("BezierEasing arguments should be integers.")}}if(mX1<0||mX1>1||mX2<0||mX2>1){throw new Error("BezierEasing x values must be in [0, 1] range.")}var mSampleValues=float32ArraySupported?new Float32Array(kSplineTableSize):[kSplineTableSize];function newtonRaphsonIterate(aX,aGuessT){for(var i=0;i<NEWTON_ITERATIONS;i+=1){var currentSlope=getSlope(aGuessT,mX1,mX2);if(currentSlope===0.0){return aGuessT}var currentX=calcBezier(aGuessT,mX1,mX2)-aX;aGuessT-=currentX/currentSlope}return aGuessT}function calcSampleValues(){for(var i=0;i<kSplineTableSize;i+=1){mSampleValues[i]=calcBezier(i*kSampleStepSize,mX1,mX2)}}function getTForX(aX){var intervalStart=0.0;var currentSample=1;var lastSample=kSplineTableSize-1;for(;currentSample!=lastSample&&mSampleValues[currentSample]<=aX;currentSample+=1){intervalStart+=kSampleStepSize}currentSample-=1;var dist=(aX-mSampleValues[currentSample])/(mSampleValues[currentSample+1]-mSampleValues[currentSample]);var guessForT=intervalStart+dist*kSampleStepSize;var initialSlope=getSlope(guessForT,mX1,mX2);if(initialSlope>=NEWTON_MIN_SLOPE){return newtonRaphsonIterate(aX,guessForT)}else if(initialSlope===0.0){return guessForT}else{return binarySubdivide(aX,intervalStart,intervalStart+kSampleStepSize)}}var _precomputed=false;function precompute(){_precomputed=true;if(mX1!=mY1||mX2!=mY2){calcSampleValues()}}var f=function(aX){if(!_precomputed){precompute()}if(mX1===mY1&&mX2===mY2){return aX;}if(aX===0){return 0}if(aX===1){return 1}return calcBezier(getTForX(aX),mY1,mY2)};f.getControlPoints=function(){return[{x:mX1,y:mY1},{x:mX2,y:mY2}]};var args=[mX1,mY1,mX2,mY2];var str="BezierEasing("+args.join()+")";f.toString=function(){return str};var css="cubic-bezier("+args.join()+")";f.toCSS=function(){return css};f.toString=function(){return args};return f}var newValues=BezierEasing(bezier[0],bezier[1],bezier[2],bezier[3]);var AniTimerange=linear(IN,start,end,0,1);return linear(newValues(AniTimerange),0,1,newStart,newEnd)}

Der Code lässt sich auf Github einsehen: cubicEase-for-After-Effects